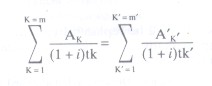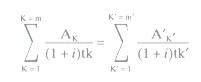STATUTORY INSTRUMENTS.

S.I. No. 294 of 2000.

EUROPEAN COMMUNITIES (CONSUMER CREDIT) REGULATIONS, 2000.

S.I. No. 294 of 2000.

EUROPEAN COMMUNITIES (CONSUMER CREDIT) REGULATIONS, 2000.

I, MARY HARNEY, Minister for Enterprise, Trade and Employment, in exercise of the powers conferred on me by section 3 of the European Communities Act, 1972 ( No. 27 of 1972 ), and for the purpose of giving effect to Directive 98/7/EC, of the European Parliament and of the Council of 16 February 1998 ¹ , hereby make the following regulations:

1. These Regulations may be cited as the European Communities (Consumer Credit) Regulations, 2000.

2. In these Regulations, the “Act” means the Consumer Credit Act, 1995 (No. 24 of 1995) .

3. Section 2 of the Act is amended in the definition of “the Council Directive”--

(a) by the substitution for “as amended by Council Directive No. 90/88/EEC of 22 February 1990⁽²⁾ ,” of “as amended by Council Directive No. 90/88/EEC of 22 February 1990⁽²⁾ and Directive 98/7/EC of the European Parliament and of the Council of 16 February 1998⁽³⁾ ,

and

(b) by the substitution, for “in Parts I and II, respectively, of the First Schedule,” of “in Parts I, II and III, respectively, of the First Schedule;”.

4. The First Schedule to the Act is amended by the insertion, after Part II of that Schedule, of Part III which is set out in part I of the Table annexed to these Regulations.

5. The Act is amended by the substitution, for the Fourth Schedule, of the schedule set out in Part 2 of the Table annexed to these Regulations.

TABLE

PART I

Part III

DIRECTIVE 98/7/EC OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 16 February 1998

amending Directive 87/102/EEC for the approximation of the laws, regulations and administrative provisions of the Member States concerning consumer credit

THE EUROPEAN PARLIAMENT AND THE COUNCIL OF THE EUROPEAN UNION,

Having regard to the Treaty establishing the European Community, and in particular Article 100a thereof,

Having regard to the proposal of the Commission⁽¹⁾ .

Having regard to the opinion of the Economic and Social Committee⁽²⁾ ,

Acting in accordance with the procedure laid down in Article 189b of the Treaty⁽³⁾

Whereas it is desirable, in order to promote the establishment and functioning of the internal market and to ensure that consumers benefit from a high level of protection, that a single method of calculating the annual percentage rate of charge for consumer credit should be used throughout the Community;

Whereas Article 5 of Directive 87/102/EEC⁽⁴⁾ provides for the introduction of a Community method or methods of calculating the annual percentage rate of charge;

Whereas, in order to introduce this single method, it is desirable to draw up a single methematical formula for calculating the annual percentage rate of charge and for determining the credit cost items to be used in the calculation by indicating those costs which must not be taken into account;

Whereas Annex II of Directive 87/102/EEC introduced a mathematical formula for the calculation of the annual percentage rate of charge and Article 1a(2) of that Directive provided for the charges to be excluded from the calculation of the ‘total cost of credit to the consumer’.

Whereas during a transitional period of three years from January 1993, Member States which prior to 1 March 1990 applied laws which permitted the use of another mathematical formula for calculating the annual percentage rate of charge, were permitted to continue to apply such laws;

Whereas the Commission has submitted a Report to the Council which makes it possible, in the light of experience, to apply a single Community mathematical formula for calculating the annual percentage rate of charge;

Whereas, since no Member State has made use of Article 1a(3) of Directive 87/102/EEC by which certain costs were excluded from the calculation of the annual percentage rate of charge in certain Member States, it has become obsolete;

Whereas accuracy to at least one decimal place is necessary;

Whereas a year is presumed to have 365 or 365,25 days or (for leap years) 366 days, 52 weeks or 12 equal months; whereas an equal month is persumed to have 30,41666 days;

Whereas it is desirable that consumers should be able to recognize the terms used different Member States to indicate the ‘annual percentage rate of charge’;

Whereas it is appropriate to study without delay to what extent a further degree of harmonization of the cost elements of consumer credit is necessary in order to put the European consumer in a position to make a better comparison between the actual percentage rates of charges offered by institutions in the various Member State, thereby ensuring harmonious functioning of the internal market,

HAVE ADOPTED THIS DIRECTIVE:

Article 1

Directive 87/102/EEC shall be amended as follows:

(a) Article 1a(1)(a) shall be replaced by the following:

--in the Greek language version of the Directive:

[illegible]

--in the English language version of the Directive:

‘The annual percentage rate of charge which shall be that rate, on an annual basis which equalizes the present value of all commitments (loans, repayments and charges), future or existing, agreed by the creditor and the borrower, shall be calculated in accordance with the mathematical formula set out in Annex II.’;

(b) Article 1a(3) shall be deleted;

(c) Article 1a(5) shall be deleted;

(d) Article 3 shall be replaced by the following:

‘Without prejudice to Council Directive 84/450/EEC of 10 September 1984 relating to the approximation of the laws, regulations and administrative provisions of the Member States concerning misleading advertising^(*) , and to the rules and principles applicable to unfair advertising, any advertisement, or any offer which is displayed at business premises, in which a person offers credit or offers to arrange a credit agreement and in which a rate of interest or any figures relating to the cost of the credit are indicated, shall also include a statement of the annual percentage rate of charge, by means of a

(e) Annex II shall be replaced by the text of Annex I representative example if no other means is practicable.

attached hereto;

(f) Annex III shall be replaced by the text of Annex II attached hereto.

Article 2

1. Member States shall bring into force the laws, regulations and administrative provisions necessary for them to comply with this Directive no later than two years after the entry into force of this Directive. They shall inform the Commission thereof.

When Member States adopt those measures, they shall contain a reference to this Directive or shall be accompained by such reference on the occasion of their official publication. The methods of making such reference shall be laid down by Member States.

2. The Member States shall communicate to the Commission the texts of the provisions of national law which they adopt in the field governed by this Directive.

Article 3

This Directive is addressed to the Member States.

Done at Brussels, 16 February 1998.

ANNEX I

‘ANNEX II

THE BASIC EQUATION EXPRESSING THE EQUIVALENCE OF LOANS ON THE ONE HAND AND REPAYMENTS AND CHARGES ON THE OTHER

Meaning of letters and symbols:

K is the number of a loan

K’ is the number of a repayment or a payment of charges

A_k is the amount of loan number K

A’_k’ is the amount of repayment number K’

Σ represents a sum

m is the number of the last loan

m’ is the number of the last repayment or payment of charges

tk’ is the interval, expressed in years and fractions of a year, between the date of loan No. 1 and those of subsequent loans Nos 2 to m

tk’ is the interval, expressed in years and fractions of a year, between the date of loan No. 1 and those of repayments or payments of charges Nos 1 to m’

i is the percentage rate that can be calculated (either by algegra, by successive approximations, or by a computer programme) where the other terms in the equation are known from the contract or otherwise.

Remarks:

(a) The amounts paid by both parties at different times shall not necessarily be equal and shall not necessarily be paid at equal intervals.

(b) The starting date shall be that of the first loan.

(c) Intervals between dates used in the calculations shall be expressed in years or in fractions of a year. A year is presumed to have 365 days or 365,25 days or (for leap years) 366 days, 52 weeks or 12 equal months. An equal month is presumed to have 30,41666 days (i.e. 365/12).

(d) The result of the calculation shall be expressed with an accuracy of at least one decimal place. When rounding to a particular decimal place the following rule shall apply:

If the figure at the decimal place following this particular decimal place is greater than or equal to 5, the figure at this particular decimal place shall be increased by one.

(e) Member States shall provide that the methods of resolution applicable give a result equal to that of the examples presented in Annex III.’

ANNEX II

‘ANNEX III

EXAMPLES OF CALCULATION

A. CALCULATION OF THE ANNUAL PERCENTAGE RATE OF CHARGE ON A CALENDAR BASIS (1 YEAR = 365 DAYS (OR 366 DAYS FOR LEAP YEARS)

First example

Sum loaned: S = ECU 1000 on 1 January 1994.

It is repaid in a single payment of ECU 1200 made on 1 July 1995 i.e. 1 1/2 years or 546 (= 365 + 181) days after the date of the loan,

or:

(1+ i)^546/365 = 1,2

1+ i = 1,1296204

i = 0,1296204

This amount will be rounded to 13% (or 12,96% if an accuracy of two decimal places is preferred).

Second example

The sum loaned is S = ECU 1,000, but the creditor retains ECU 50 for administrative expenses, so that the loan is in fact ECU 950; the repayment of ECU 1,200, as in the first example, is again made on 1 July 1995.

or:

(1+ i)^546/365 = 1,263157

1+ i = 1,169026

i = 0,169026

This amount will be rounded to 16,9%.

Third example

The sum loaned is ECU 1,000, on 1 January 1994, repayable in two amounts, each ECU 600, paid after one and two years respectively.

The equation becomes:

It is solved by algebra and produces i=0,1306623 rounded to 13,1% (or 13,07% if an accuracy of two decimal places is preferred).

Fourth example

The sum loaned is S= ECU 1,000, on 1 January 1994, and the amounts to be paid by the borrower are:

The equation becomes:

This equation allows i to be calculated by successive approximations, which can be programmed on a pocket calculation.

The result is i=0,13226 rounded to 13.2% (or 13,23% if an accuracy of two decimal places is preferred).

B. CALCULATION OF THE ANNUAL PERCENTAGE RATE OF CHARGE ON THE BASIS OF A STANDARD YEAR (1 YEAR = 365 DAYS OR 365,25 DAYS, 52 WEEKS, OR 12 EQUAL MONTHS)

First example

Sum loaned: S = ECU 1,000

It is repaid in a single payment of ECU 1,200 made in 1.5 years (i.e. 1,5 x 365=547,5 days, 1,5 x 365,25 = 547,875 days, 1.5 x 366 = 549 days, 1,5 x 12 = 18 months, or 1,5 x 52 =78 weeks) after the date of the loan.

The equation becomes:

or:

(1+ i)^1,5 = 1,2

1+ i = 1,129243

i = 0,129243

This amount will be rounded to 12,9% (or 12,92% if an accuracy of two decimal places is preferred).

Second example

The sum loaned is S = ECU 1,000, but the creditor retains ECU 50 for administrative expenses, so that the loan is in fact ECU 950; the repayment of ECU 1,200, as in the first example, is again made 1.5 years after the date of the loan.

The equation becomes:

or:

(1+ i)^1,5 = 1200/950 = 1,263157

1+ i = 1,168526

i = 0,168526

This amount will be rounded to 16.9% (or 16.85% if an accuracy of two decimal places is preferred).

Third example

The sum loaned is ECU 1,000, repayable in two amounts, each of ECU 600, paid after one and two years respectively.

The equation becomes

It is solved by algebra and produces i = 0,13066 which will be rounded to 13,1% (or 13,07% if an accuracy of two decimal places is preferred).

Fourth example

The sum loaned is S = ECU 1,000 and the amounts to be paid by the borrower are:

The equation becomes:

This equation allows i to be calculated by successive approximations, which can be programmed on a pocket calculator. The result is i = 0,13185 which will be rounded to 13,2% (or 13,19% if an accuracy of two decimal places is preferred).

PART II

Fourth Schedule

APR - METHOD OF CALCULATION

THE BASIC EQUATION EXPRESSING THE EQUIVALENCE OF LOANS ON THE ONE HAND AND REPAYMENTS AND CHARGES ON THE OTHER

Meaning of letters and symbols:

K is the number of a loan

K’ is the number of a repayment or a payment of charges

A_k is the amount of loan number K

A’_k’ is the amount of repayment number K’

Σ represents a sum

m is the number of the last loan

m’ is the number of the last repayment or payment of charges

tk is the interval, expressed in years and fractions of a year, between the date of loan No. 1 and those of subsequent loans Nos 2 to m

tk’ is the interval, expressed in years and fractions of a year, between the date of loan No. 1 and those of repayments or payments of charges Nos 1 to m’

i is the percentage rate that can be calculated (either by algegra, by successive approximations, or by a computer programme) where the other terms in the equation are known from the contract or otherwise.

Remarks:

(a) The amounts paid by both parties at different times shall not necessarily be equal and shall not necessarily be paid at equal intervals.

(b) The starting date shall be that of the first loan.

(c) Intervals between dates used in the calculations shall be expressed in years or in fractions of a year. A year is presumed to have 365 days or 365,25 days or (for leap years) 366 days, 52 weeks or 12 equal months. An equal month is presumed to have 30,41666 days (i.e. 365/12).

(d) The result of the calculation shall be expressed with an accuracy of at least one decimal place. When rounding to a particular decimal place the following rule shall apply:

If the figure at the decimal place following this particular decimal place is greater than or equal to 5, the figure at this particular decimal place shall be increased by one.

(e) Member States shall provide that the methods of resolution applicable give a result equal to that of the examples presented in Annex III.’

EXPLANATORY NOTE

(This note is not part of the Instrument and does not purport to be a legal interpretation.)

The purpose of these Regulations is to give effect to Council Directive 98/7/EC. This Directive amends certain provisions of Council Directive 87/102/EEC, concerning consumer credit. The principal amendments relate to the method of calculation of the annual percentage rate of charge for credit (APR) and consists of additional direction and illustrative examples as how to apply the mathematical formula for calculating the APR.

¹ O.J. No. L101, 1.4.98, p17.

⁽²⁾ O.J. No. C30, 30.1.1997, p.94.

⁽²⁾ O.J. No. C30, 30.1.1997, p.94.

⁽³⁾ O.J. No. L101, 1.4.98, p17,”

⁽¹⁾ O.J. No. C235, 13.8.1996, p.8 and O.J. No. C137, 3.5.1997, p.9.

⁽²⁾ O.J. No. C30, 30.1.1997, p.94.

⁽³⁾ Opinion of the European Parliament of 20 February 1997 (O.J. No. C85, 17.3.1997, p. 108), Council Common Position of 7 July 1997 (O.J. No. C284, 19.9.1997, p.1) and Decision of the European Parliament of 19 November 1997, Council Decision of 18 December 1997.

⁽⁴⁾ O.J. No. L42, 12.2.1987, p.48 directive as amended by Directive 90/88/EEC (O.J. No. L61, 10.3.1990, p.14).

^(*) O.J. No. L250, 19.9.1984, p.17. Directive as last amended by Directive 97/55/EC (O.J. No. L280, 23.10.1997, p.18).