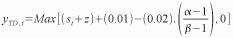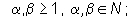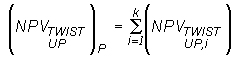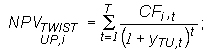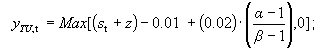S.I. No. 612 of 2007

ASSET COVERED SECURITIES ACT 2001 (SECTION 91(1)) (SENSITIVITY TO INTEREST RATE CHANGES - MORTGAGE CREDIT) (AMENDMENT) REGULATIONS 2007

Notice of the making of this Statutory Instrument was published in

�Iris Oifigi�il� of 7th September, 2007.

In exercise of the powers conferred on the Authority by section 91(1) of the Asset Covered Securities Act 2001 (No. 47 of 2001) (the �Act�), the Irish Financial Services Regulatory Authority, in performance of the functions of the Authority in accordance with section 33C(1)(a) of the Central Bank Act 1942 (No. 22 of 1942), hereby makes the following regulations:

1. These regulations may be cited as the Asset Covered Securities Act 2001 (Section 91(1)) (Sensitivity to Interest Rate Changes - Mortgage Credit) (Amendment) Regulations 2007.

2. The Schedule to the Asset Covered Securities Act, 2001 (Section 91(1)) (Sensitivity to Interest Rate Changes) Regulation, 2004 ( S.I. No. 416 of 2004 ) is repealed and substituted by the Schedule to these regulations.

Signed for and on behalf of

THE IRISH FINANCIAL SERVICES REGULATORY AUTHORITY

31 August 2007

Mr. PATRICK NEARY

Chief Executive

Irish Financial Services Regulatory Authority

SCHEDULE FORMULAE IN RESPECT OF SECTION 91(1)

(SENSITIVITY TO INTEREST RATE CHANGES - MORTGAGE CREDIT) REGULATION

This schedule sets out the formulae to be used by designated mortgage credit institutions in measuring sensitivity to interest rate changes.

In this schedule, unless the context otherwise requires, �relevant exposure� means a mortgage credit asset, hedge contract, mortgage covered security issued, substitution asset, pool hedge collateral or any other asset or position held that is sensitive to interest rate changes.

1. Calculation of net present values

1.1 Fixed Interest Rate Assets

The net present value of a relevant exposure, the interest payable on which is fixed, shall be calculated as the sum of the present values of each cashflow payable on the relevant exposure in each time period, as follows:

where

CFt = Interestt + Capitalt

st is the zero coupon interest rate, derived from the appropriate swap curve, at valuation, to time t

z is a static spread over the zero coupon interest rate, derived from the appropriate swap curve, that lets the net present value of the relevant exposure be equal to its price.

1.2 Floating interest rate assets

The net present value of a relevant exposure, the interest payable on which is floating, shall be calculated as the discounted value of the principal or notional principal and interest outstanding from the next payment date, as follows:

where

where

P0 is principal outstanding at the valuation date, time zero

t time in years (or part of a year) to the next re-pricing date

r is the annualised rate on the relevant exposure on a simple interest basis

st the annualised Euribor or Libor zero-coupon rate, derived from the appropriate swap curve, to maturity t

x a constant spread to the Euribor or Libor zero coupon rate, derived from the appropriate swap curve, that discounts the cash flows to par.

1.3 Fixed interest rate hedge contracts or mortgage covered securities issued.

Subject to paragraph 1.6, the net present value of a hedge contract or mortgage covered security issued, the interest payable on which is fixed, shall be calculated as the sum of the present values of each cashflow payable on the contract or security in each time period, as follows:

where

CFt = Interestt + Capitalt

st is the zero coupon interest rate, derived from the appropriate swap curve, at valuation, to time t

z is a static spread over the zero coupon interest rate, derived from the appropriate swap curve, that lets the net present value of the contract or security be equal to its price.

1.4 Floating interest rate hedge contracts or mortgage covered securities issued

Subject to paragraph 1.6, the net present value of a hedge contract or mortgage covered security issued, the interest payable on which is floating, shall be calculated as the discounted value of the principal or notional principal and interest outstanding from the next payment date, as follows:

where

where

P0is principal outstanding at the valuation date, time zero

ttime in years (or part of a year) to the next re-pricing date

ris the annualised rate on the contract or security on a simple interest basis

st is the zero coupon interest rate, derived from the appropriate swap curve, at valuation, to time t; and

x is a static spread over the zero coupon interest rate, derived from the appropriate swap curve, that lets the net present value of the contract or security be equal to its price.

1.5 Total net present value of all relevant exposures

The total net present value of all relevant exposures shall be calculated as the sum of the net present values of the relevant exposures.

1.6 Hedge contracts

Where a hedge contract has a notional amount equal to the outstanding principal (or nominal) from time to time of mortgage credit assets and/or substitution assets which are cover assets, or as applicable, not cover assets from time to time and that hedge contract has the hedging effect of converting a blended or averaged interest rate (determined by reference to various interest rates payable on those assets) into a single floating or fixed interest rate, that hedge contract shall be treated for the net present value purposes together with the related mortgage credit assets and/or substitution assets as a single floating rate relevant exposure or, as applicable, single fixed rate relevant exposure.

Where a hedge contract has a notional amount equal to the outstanding principal (or nominal) and term of one or more issues of mortgage covered securities and that hedge contract has the hedging effect of converting the interest rate payable on those mortgage covered securities into a single floating or fixed rate, that hedge contract shall be treated for net present value purposes together with the related mortgage covered securities as a single floating rate asset or, as applicable, single fixed rate asset.

The net present value of any other hedge contract shall be calculated, as appropriate, on the basis of the applicable formulae set out in paragraph 1.3 or 1.4.

2. Measurement of sensitivity to interest rate changes

Designated mortgage credit institutions shall use the following methodology in measuring their sensitivity to changes in interest rates.

2.1 Upward parallel shift in the yield curve

For a one hundred basis points upward shift in the yield curve, the resultant net present value of relevant exposures shall be calculated as follows:

where, for an individual relevant exposure, i:

;

;

st = zero coupon interest rate, derived from the appropriate swap curve, at valuation to time t;

z is a static spread over the zero coupon interest rate, derived from the appropriate swap curve, that lets the net present value of the relevant exposure be equal to its price.

2.2 Downward parallel shift in the yield curve

For a one hundred basis points downward shift in the yield curve, the resultant net present value of relevant exposures shall be calculated as:

where, for an individual relevant exposure, i

st = zero coupon interest rate, derived from the appropriate swap curve, at valuation, to time t,

z is the static spread over the zero coupon interest rate, derived from the appropriate swap curve, that lets the net present value of the relevant exposure be equal to its price.

2.3 Changes in the slope of the yield curve

2.3.1 General approach

The procedure for the calculation of the net present value of relevant exposures resulting from a one hundred basis points twist in the yield curve shall be as follows:

�for all revaluation points along the yield curve up to and including 3 months (i.e. the �short end�), increase (decrease) the yield curve values by 100 basis points;

�for all revaluation points along the yield curve greater than or equal to 10 years (i.e. the �long end�), decrease (increase) the yield curve values by 100 basis points; and

�in the interval from 3 months to 10 years, make proportional changes to the yield curve in accordance with the number of revaluation points in the interval.

This new yield curve shall then be applied to all relevant exposures. The formulae for the calculation of the net present value of all relevant exposures resulting from a one hundred basis points twist in the yield curve are set out in paragraphs 2.3.2 and 2.3.3.

2.3.2 Downward change in the slope of the yield curve

For a twist in the yield curve, up one hundred basis points in the short term and down one hundred basis points in the long term, with proportional changes in the interval, the resultant net present value of relevant exposures shall be calculated as:

where, for an individual relevant exposure, i:

= 1 for t 3 months;

= for t 10 years;

for 3 months t 10 years, assign ascending values of to each revaluation point along the curve greater than 3 months and less than 10 years, beginning with = 1 for t = 3 months;

is the final revaluation point along the curve required in the interval (3 months t 10 years);

z is a static spread over the zero coupon interest rate, derived from the appropriate swap curve, that lets the net present value of the relevant exposure be equal to its price.

2.3.3 Upward change in the slope of the yield curve

For a twist in the yield curve, down one hundred basis points in the short term and up one hundred basis points in the long term, with proportional changes in the interval, the resultant net present value of relevant exposures shall be calculated as:

where, for an individual relevant exposure, i:

= 1 for t 3 months;

= for t 10 years;

for 3 months t 10 years, assign ascending values of to each revaluation point along the curve greater than 3 months and less than 10 years, beginning with = 1 for t = 3 months;

is the final revaluation point along the curve required in the interval (3 months t 10 years);

z is a static spread over the zero coupon interest rate, derived from the appropriate swap curve, that lets the net present value of the relevant exposure be equal to its price.

2.4 Sensitivity to changes in interest rates

Sensitivity to changes in interest rates shall be measured as the difference between:

�actual net present value and the resultant net present value from a one hundred basis point upward shift in the yield curve;

�actual net present value and the resultant net present value from a one hundred basis point downward shift in the yield curve;

�actual net present value and the resultant net present value from a twist in the yield curve of plus one hundred basis points in the short term and minus one hundred basis points in the long term, with proportional changes in the interval; and

�actual net present value and the resultant net present value from a twist in the yield curve of minus one hundred basis points in the short term and plus one hundred basis points in the long term, with proportional changes in the interval.

3. Reference interest rate curve

The appropriate interest rate swap curve for each currency shall be used as the reference curve for valuing all relevant exposures.

EXPLANATORY NOTE

(This note is not part of the Instrument and does not purport to be a legal interpretation.)

These regulations substitute the Schedule in the Asset Covered Securities Act, 2001 (Section 91(1)) (Sensitivity to Interest Rate Changes) Regulation, 2004 ( S.I. No. 416 of 2004 ) with the Schedule in these regulations.
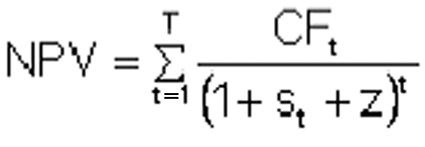